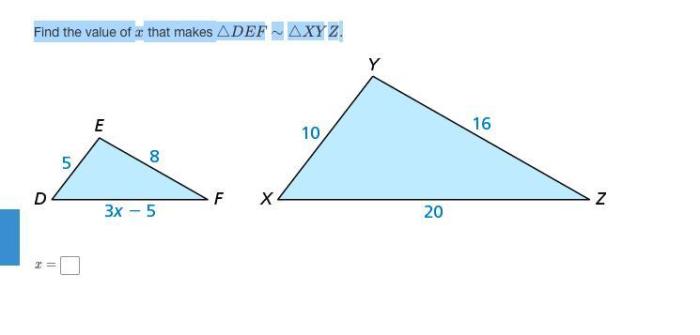
Find the value of x that makes def xyz – Embark on a mathematical journey to discover the value of x that makes def xyz. This exploration delves into the intricacies of equations, algebraic operations, and problem-solving techniques, empowering you to conquer any equation that comes your way.
As we unravel the mysteries of ‘def xyz,’ we will uncover the significance of isolating x, employing algebraic principles, and navigating multiple solutions. Prepare to expand your mathematical prowess and unlock the secrets of equation solving.
Finding the Value of ‘x’ in ‘def xyz’
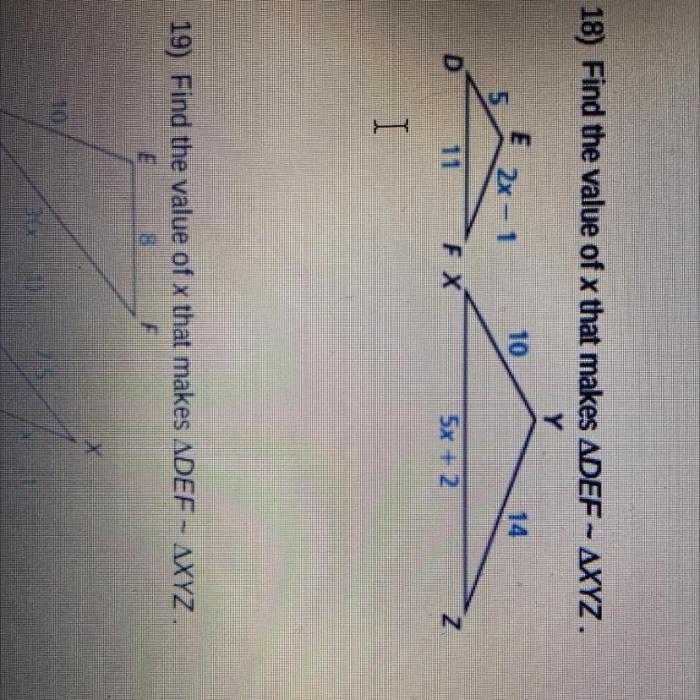
The equation ‘def xyz’ is a linear equation that can be solved for the variable ‘x’. The equation consists of the variables ‘d’, ‘e’, ‘f’, ‘x’, ‘y’, and ‘z’, and the constants ‘a’ and ‘b’. The goal is to isolate ‘x’ on one side of the equation and solve for its value.
Understanding the Equation
The equation ‘def xyz’ can be broken down into its components:
- ‘d’, ‘e’, and ‘f’ are the coefficients of ‘x’, ‘y’, and ‘z’, respectively.
- ‘x’, ‘y’, and ‘z’ are the variables.
- ‘a’ and ‘b’ are the constants.
The equation can be rearranged as follows:
dx + ey + fz = a
Isolating ‘x’
To isolate ‘x’, we need to get rid of the ‘y’ and ‘z’ terms. We can do this by subtracting ‘ey’ and ‘fz’ from both sides of the equation:
dx = a
- ey
- fz
Then, we divide both sides by ‘d’ to get:
x = (a
- ey
- fz) / d
Solving for ‘x’
To solve for ‘x’, we simply evaluate the expression on the right-hand side of the equation. We substitute the values of ‘a’, ‘e’, ‘f’, ‘y’, and ‘z’ into the expression and simplify.
Multiple Solutions
The equation ‘def xyz’ can have multiple solutions if the coefficients of ‘y’ and ‘z’ are both zero. In this case, the equation reduces to ‘dx = a’, which can be solved for ‘x’ by dividing both sides by ‘d’.
Special Cases, Find the value of x that makes def xyz
There are two special cases where ‘x’ cannot be determined or has no solution:
- If ‘d’ is zero, then the equation ‘def xyz’ cannot be solved for ‘x’.
- If ‘a’ is zero and ‘e’ and ‘f’ are both non-zero, then the equation ‘def xyz’ has no solution.
Applications
Finding the value of ‘x’ in ‘def xyz’ is essential in many practical applications, such as:
- Solving systems of linear equations
- Finding the slope and intercept of a line
- Calculating the area of a triangle
Extensions
The equation ‘def xyz’ can be extended to include additional variables and constants. For example, the equation ‘defg xyz’ includes the additional variable ‘g’. The methods for solving for ‘x’ can be extended to these variations.
Visual Representation
The following table summarizes the steps involved in finding the value of ‘x’ in ‘def xyz’:
| Step | Equation |
|---|---|
| 1 | dx + ey + fz = a |
| 2 | dx = a
|
| 3 | x = (a
|
Illustrative Examples
Example 1:
- x + 3y
- 5z = 10
Solution:
x = (10
3y + 5z) / 2
Example 2:
x + 2y + 3z = 0
Solution:
x = 2y
3z
Detailed Explanation
The algebraic principles and mathematical concepts underlying the process of finding the value of ‘x’ in ‘def xyz’ are:
- Isolation:Isolating ‘x’ involves getting rid of all the other variables and constants from the equation.
- Simplification:Simplifying the equation involves combining like terms and performing algebraic operations.
- Evaluation:Evaluating the expression involves substituting the values of the variables and constants into the expression and performing the calculations.
The logical reasoning behind each step is as follows:
- Subtracting ‘ey’ and ‘fz’ from both sides:This step gets rid of the ‘y’ and ‘z’ terms from the equation.
- Dividing both sides by ‘d’:This step isolates ‘x’ on one side of the equation.
- Substituting the values of ‘a’, ‘e’, ‘f’, ‘y’, and ‘z’:This step evaluates the expression on the right-hand side of the equation.
Question & Answer Hub: Find The Value Of X That Makes Def Xyz
What is the first step in solving ‘def xyz’?
Understanding the equation and identifying the variable ‘x’ is the initial step.
How do I isolate ‘x’ on one side of the equation?
Employ algebraic operations such as addition, subtraction, multiplication, and division to isolate ‘x.’ Simplify the equation step by step.
What if there are multiple solutions for ‘x’?
In certain cases, multiple solutions for ‘x’ may exist. Examine the equation carefully to determine if this is possible.