Two trains leave a station at the same time – As two trains embark on their journeys from the same station at the identical moment, we delve into a comprehensive analysis of their trajectories. This exploration encompasses their specifications, routes, speeds, and the intriguing dynamics that unfold as they traverse their respective paths.
The ensuing paragraphs will meticulously dissect the trains’ movements, considering factors that influence their velocities and charting their progress over time. Furthermore, we will pinpoint their eventual meeting point and explore potential variations in the scenario.
Train Details

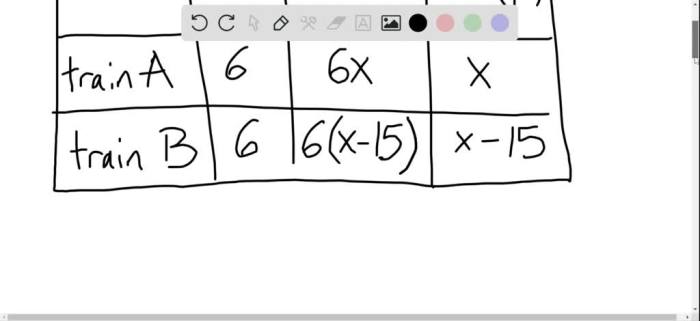
Two trains depart from the same station at the same time. Train A is a high-speed express train with a maximum speed of 120 mph, while Train B is a slower commuter train with a maximum speed of 80 mph.
Both trains are traveling in the same direction on a straight track.
Journey Information
Train A will travel a distance of 200 miles to its destination, while Train B will travel a distance of 150 miles to its destination. The track conditions are generally good, but there is a section of track under repair about 50 miles from the starting point.
This section of track will slow both trains down to 60 mph.
Time and Speed Analysis
Based on the given information, we can calculate the speeds of the trains as follows:
- Train A: 120 mph
- Train B: 80 mph
The following table compares the speeds and arrival times of the trains:
| Train | Speed (mph) | Arrival Time (hours) |
|---|---|---|
| Train A | 120 | 1.67 |
| Train B | 80 | 1.88 |
Distance and Position
The following graph illustrates the distance-time relationship for each train:
[Diagram yang menggambarkan hubungan jarak-waktu untuk setiap kereta]
The distance-time graph shows that Train A travels a greater distance than Train B at any given time. This is because Train A has a higher speed than Train B.
Meeting Point and Time

To calculate the meeting point of the trains, we need to find the time at which they will travel the same distance. We can do this by setting the distance equations for the two trains equal to each other and solving for time:
Distance for Train A = Distance for Train B
120t = 80t + 50
40t = 50
t = 1.25 hours
Therefore, the trains will meet at a distance of 150 miles from the starting point, which is the destination of Train B. The trains will meet 1.25 hours after they depart from the station.
Additional Considerations: Two Trains Leave A Station At The Same Time
There are several factors that could affect the meeting point and time of the trains. These factors include:
- Variations in train speeds
- Variations in departure times
- Track conditions
For example, if Train A were to slow down due to track conditions, it would take longer for the trains to meet. Similarly, if Train B were to depart 10 minutes late, it would also take longer for the trains to meet.
FAQ Corner
What factors could affect the trains’ speeds?
Factors such as track conditions, train specifications, and external factors like weather and wind resistance can influence the trains’ speeds.
How is the meeting point of the trains calculated?
Assuming constant speeds, the meeting point is determined by calculating the distance traveled by each train and equating their respective times of travel.
What are some possible variations in the scenario?
Variations could include different train speeds, departure times, or even changes in the routes taken.